Cách chứng minh tứ giác nội tiếp
Chứng minh tứ giác nội tiếp là việc chúng ta cần chứng minh 4 đỉnh của tứ giác nằm trên cùng một đường tròn. Đây là dạng bài tập sẽ có nhiều mức độ để thử thách các em học sinh có học lực từ trung bình đến giỏi.
Chính vì vậy trong bài viết dưới đây THPT Nguyễn Đình Chiểu xin giới thiệu đến các bạn toàn bộ kiến thức về tứ giác nội tiếp như khái niệm, định lí, dấu hiệu nhận biết, cách chứng minh tứ giác nội tiếp. Thông qua tài liệu này các bạn có thêm nhiều gợi ý ôn tập, củng cố kiến thức để nhanh chóng biết giải các bài tập toán để đạt kết quả cao trong kì thi vào lớp 10 sắp tới.
Bạn đang xem: Cách chứng minh tứ giác nội tiếp
1. Tứ giác nội tiếp là gì?
Một tứ giác có bốn đỉnh nằm trên một đường tròn gọi là tứ giác nội tiếp đường tròn (gọi tắt là tứ giác nội tiếp).
Lúc này, đường tròn được gọi là đường tròn ngoại tiếp, và các đỉnh của tứ giác được gọi là đồng viên.

2. Định lý của tứ giác nội tiếp
Trong một tứ giác nội tiếp, tổng số đo hai góc đối diện bằng 180°.
Ngược lại, nếu một tứ giác có tổng số đo hai góc đối diện bằng 180° thì tứ giác đó nội tiếp được đường tròn.
3. Dấu hiệu nhận biết tứ giác nội tiếp đường tròn
– Tứ giác có tổng số đo của hai góc đối bằng 180 độ thì tứ giác đó nội tiếp đường tròn.
– Tứ giác có góc ngoài tại một đỉnh bằng với góc trong tại đỉnh đối của nó thì tứ giác đó nội tiếp đường tròn.
– Tứ giác có 4 đỉnh cách đều một điểm mà ta có thể xác định được, điểm đó chính là tâm của đường tròn ngoại tiếp.
– Tứ giác có hai đỉnh kề nhau, hai đỉnh này cùng nhìn cạnh chứa hai đỉnh còn lại dưới một góc α thì tứ giác đó nội tiếp đường tròn.
4. Cách chứng minh tứ giác nội tiếp
Phương pháp 1: Chứng minh bốn đỉnh của tứ giác cách đều 1 điểm
Ví dụ: Cho nửa đường tròn tâm O đường kính AB = 2R và tia tiếp tuyến Ax cùng phía với nửa đường tròn đối với AB. Từ điểm M trên Ax kẻ tiếp tuyến thứ hai MC với nửa đường tròn (C là tiếp điểm). AC cắt OM tại E, MB cắt nửa đường tròn (C) tại D (D khác B)
Chứng minh rằng: Tứ giác AMCO và AMDE là các tứ giác nội tiếp đường tròn.
Hướng dẫn giải
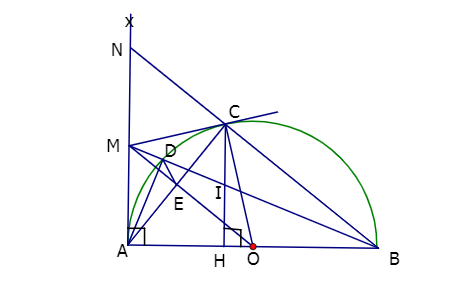
Vì MA, MB, MC là các tiếp tuyến
=>
=> Tứ giác AMCO nội tiếp đường tròn đường kính MO.
Ta có (góc nội tiếp chắn nửa đường tròn)
=>
Ta lại có: OA = OC = R, MA = MC
=> MO là đường trung trực của AC
=>
Từ (*) và (**) => AMDE là tứ giác nội tiếp đường tròn đường kính MA.
Phương pháp 2: Chứng minh tứ giác có hai góc đối diện bù nhau (tổng hai góc đối diện bằng 1800)
Ví dụ: Cho đường tròn (O; R) AB và CD là hai đường kính khác nhau của đường tròn. Tiếp tuyến tại B của đường tròn (O, R) cắt các đường thẳng AC, AD theo thứ tự tại E và F.
a) Chứng minh rằng tứ giác ACBD là hình chữ nhật
b) Chứng minh tam giác ACD và tam giác CBE đồng dạng
c) Chứng minh tứ giác CDEF nội tiếp được đường tròn
Hướng dẫn giải
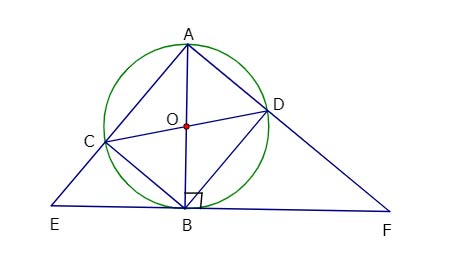
a) Tứ giác ACBD có hai đường chéo AB và CD bằng nhau và cắt nhau tại trung điểm của mỗi đường, suy ra ACBD là hình chữ nhật.
b) Tứ giác ACBD là hình chữ nhật
=> (1)
Ta lại có:
Mà sd BC = sd AD (2)
Từ (1) và (2) =>
c) Vì ACBD là hình chữ nhật nên CB song song với AF
=> (3)
Từ (2) và (3) => do đó tứ giác CDFE nội tiếp được đường tròn.
Phương pháp 3: Chứng minh hai đỉnh cùng nhìn đoạn thẳng tạo bởi hai điểm còn lại hai góc bằng nhau.
Ví dụ: Từ một điểm A nằm bên ngoài đường tròn (O; R) ta vẽ hai tiếp tuyến AB và AC với đường tròn (B, C) là tiếp điểm). Trên cung nhỏ BC lấy điểm M, vẽ MI vuông góc với AB, MK vuông góc với AC (I thuộc AB, K thuộc AC)
a) Chứng minh AIMK là tứ giác nội tiếp đường tròn.
b) Kẻ MP vuông góc BC (P thuộc BC). Chứng minh:
Hướng dẫn giải

a) Ta có:
=> Tứ giác AIMK nội tiếp đường tròn đường kính AM.
b) Tứ giác CPMK có:
Do đó CPMK là tứ giác nội tiếp
=>
Vì CK là tiếp tuyến của (O) nên ta có:
=>
Phương pháp 4: Chứng minh bằng phương pháp phản chứng
Có thể chứng minh tứ giác ABCD là một trong những hình đặc biệt sau: Tứ giác ABCD là hình thang cân, hình chữ nhật, hình vuông.
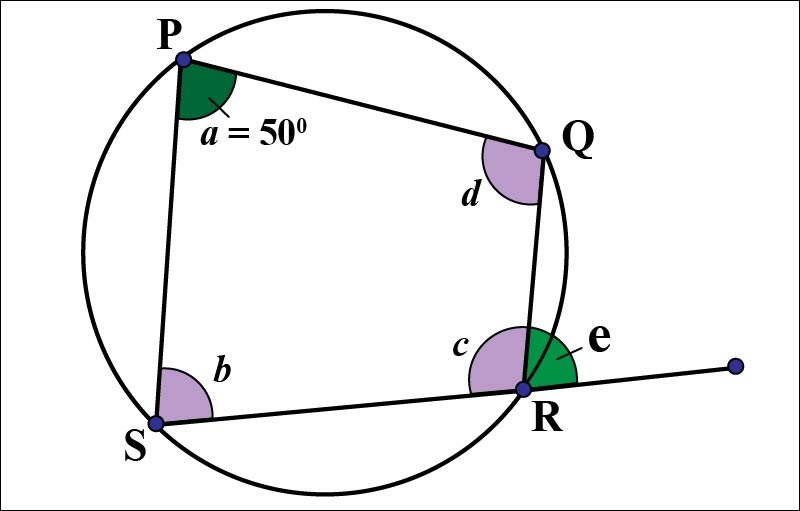
Phương pháp 5: Chứng minh qua góc ngoài của tứ giác
Ví dụ: Cho tứ giác ABCD, nếu chứng minh được góc ngoài tại đỉnh A bằng góc trong tại đỉnh C (tức là góc C của tứ giác đó) thì tứ giác ABCD nội tiếp đường tròn.
Đăng bởi: THPT Nguyễn Đình Chiểu
Chuyên mục: Tài Liệu Lớp 9












