Cách chứng minh tiếp tuyến của đường tròn

Tiếp tuyến của đường tròn là gì? Cách chứng minh tiếp tuyến của đường tròn như thế nào? Mời quý thầy cô cùng các bạn học sinh lớp 9 theo dõi bài viết dưới đây của THPT Nguyễn Đình Chiểu nhé.

Trong bài viết dưới đây THPT Nguyễn Đình Chiểu sẽ giới thiệu đến các bạn toàn bộ kiến thức về cách chứng minh tiếp tuyến của đường tròn và một số bài tập kèm theo. Thông qua tài liệu này giúp các bạn học sinh có thêm nhiều tư liệu ôn tập, củng cố kiến thức làm quen với các dạng bài tập Hình học. Bên cạnh đó các bạn xem thêm công thức tính chu vi hình chữ nhật, công thức tính diện tích hình vuông.

Bạn đang xem: Cách chứng minh tiếp tuyến của đường tròn

Cách chứng minh tiếp tuyến của đường tròn

1. Cách chứng minh tiếp tuyến của đường tròn

– Cách 1: Chứng minh đường thẳng d vuông góc với bán kính của đường tròn.

– Cách 2: Chứng minh khoảng cách từ tâm O của đường tròn đến đường thẳng d bằng bán kính R của đường tròn.

– Cách 3: Chứng minh hệ thức MA² = MB.MC thì MA là tiếp tuyến của đường tròn ngoại tiếp tam giác ADE.

2. Ví dụ chứng minh tiếp tuyến của đường tròn

Ví dụ 1 : Cho ΔABC nội tiếp đường tròn (O), (AB < AC). Trên tia đối của tia BC lấy điểm M sao cho MA² = MB.MC. Chứng minh rằng: MA là tiếp tuyến của đường tròn (O).

Gợi ý đáp án

Vẽ hình minh họa:

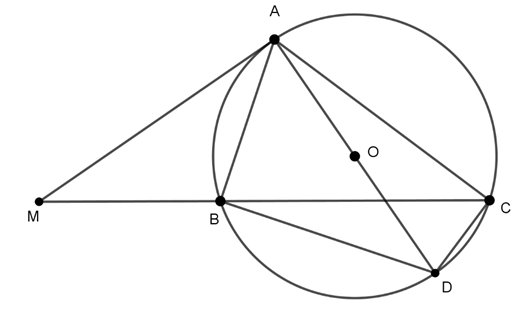
Vì MA² = MB.MC ⇒

Xét ΔMAC và ΔMBA có

: góc chung

⇒ ΔMAC ∼ ΔMBA (c.g.c)

 (1)

Kẻ đường kính AD của (O)

Ta có  (hai góc nội tiếp cùng chắn cung AB )

Mà  (chứng minh trên)

Suy ra   (3)

Lại có =90^o  (góc nội tiếp chắn nửa đường tròn)

=  90^o (4)

Từ (3) và (4) suy ra = 90^o hay = 90^o

⇒ OA ⊥ MA

Do A ∈ (O)

⇒ MA là tiếp tuyến của (O).

Ví dụ 2: Cho tam giác ABC nhọn. Vẽ đường tròn tâm O đường kính BC, cắt AB,AC lần lượt tại E và F. BF và CE cắt nhau tại I. Gọi M là trung điểm của AI. Chứng minh MF là tiếp tuyến của (O).

Gợi ý đáp án

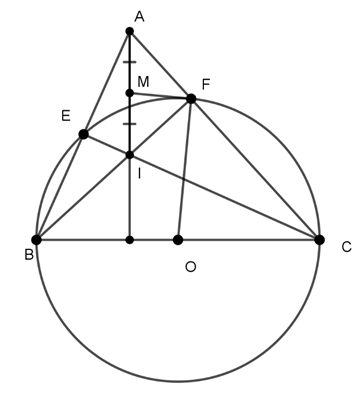
Ta có : (góc nội tiếp chắn nửa đường tròn)

⇒ BF ⊥ AC , CE ⊥ AB

Xét tam giác ABC, có BF ∩ CE = {I}

⇒ I là trực tâm tam giác ABC

Gọi H là giao điểm của AI với BC

⇒ AH ⊥ BC tại H

Xét tam giác AFI vuông tại F, có M là trung điểm của AI

⇒ FM = MA = MI

⇒ ΔFMA cân tại M

(hai góc ở đáy) (1)

Xét tam giác OFC, có OF = OC

⇒ FOC cân tại O

⇒   (hai góc ở đáy) (2)

Xét tam giác AHC vuông tại H, có: = 90^o (hai góc phụ nhau)(3)

Từ (1), (2) và (3)  = 90^O

Mà = 90^O

⇒ MF ⊥ OF

Vậy MF là tiếp tuyến của (O).

Đăng bởi: THPT Nguyễn Đình Chiểu

Chuyên mục: Tài Liệu Lớp 9