Giải Toán 7 Bài 8: Các trường hợp bằng nhau của tam giác vuông
Giải toán 7 Bài 8: Các trường hợp bằng nhau của tam giác vuông giúp các em học sinh lớp 7 tham khảo cách giải bài tập 63, 64, 65, 66 trang 136, 137 sách giáo khoa Toán lớp 7 tập 1.
Tài liệu được biên soạn chi tiết rõ ràng, bám sát chương trình học Toán 7. Qua đó giúp học sinh lớp 7 tham khảo nắm vững hơn kiến thức trên lớp. Bên cạnh đó các bạn tham khảo thêm Bộ đề kiểm tra 1 tiết Chương II Hình học lớp 7. Mời các bạn cùng theo dõi bài tại đây.
Bạn đang xem: Giải Toán 7 Bài 8: Các trường hợp bằng nhau của tam giác vuông
Lý thuyết Các trường hợp bằng nhau của tam giác vuông
A. Khái niệm hai tam giác bằng nhau
Hai tam giác bằng nhau là hai tam giác có các cạnh tương ứng bằng nhau, các góc tương ứng bằng nhau.
Để kí hiệu sự bằng nhau của tam giác ABC và tam giác A’B’C”.

B. Các trường hợp bằng nhau của tam giác vuông
*Hai cạnh góc vuông
Nếu hai cạnh góc vuông của tam giác vuông này lần lượt bằng hai cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau (cạnh – góc – cạnh )

*Cạnh góc vuông và góc nhọn kề cạnh đó
Nếu một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông này bằng một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông kia thì hai tam giác vuông đó bằng nhau ( góc – cạnh – góc )

*Cạnh huyền – góc nhọn
Nếu cạnh huyền và một góc nhọn của tam giác vuông này bằng cạnh huyền và một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó bằng nhau ( góc – cạnh – góc)

*Cạnh huyền – cạnh góc vuông
Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này bằng cạnh huyền và một cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.

Giải bài tập Toán 7 trang 136 Tập 1
Bài 63 (trang 136 – SGK Toán lớp 7 Tập 1)
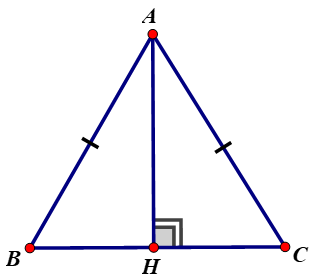
Cho tam giác ABC cân tại A. Kẻ AH vuông góc với BC. Chứng minh rằng
a) HB = HC
b) góc BAH = góc CAH
a) Xét hai tam giác vuông ΔABH và ΔACH có:
AB = AC (giả thiết)
AH cạnh chung
⇒ ΔABH = ΔACH (cạnh huyền – cạnh góc vuông)
Suy ra HB = HC (cặp cạnh tương ứng)
b) Ta có ΔABH = ΔACH (chứng minh trên)
(cặp góc tương ứng)
Bài 64 (trang 136 – SGK Toán lớp 7 Tập 1)
Các tam giác vuông ABC và DEF có góc A = góc D = 90o, AC = DF. Hãy bổ sung thêm một điều kiện bằng nhau để ΔABC = ΔDEF.

+ Bổ sung AB =DE thì ΔABC = ΔDEF (cạnh – góc – cạnh)
+ Bổ sung thì ΔABC = ΔDEF (góc – cạnh – góc)
+ Bổ sung BC = EF thì ΔABC = ΔDEF (cạnh huyền – cạnh góc vuông)
Giải bài tập Toán 7 trang 131: Luyện tập
Bài 65 (trang 137 – SGK Toán lớp 7 Tập 1)
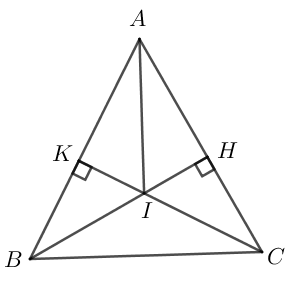
Cho ΔABC cân ở A (∠A < 90o). Vẽ BH ⊥ AC (H ∈ AC), CK ⊥ AB (K ∈ AB).
a) Chứng minh rằng AH = HK
b) Gọi I là giao điểm của BH và CK. Chứng minh rằng AI là tia phân giác của góc A
a) ΔABC cân tại A (giả thiết)
Suy ra
AB = AC (tính chất)
(định lí)
Xét hai tam giác vuông HAB và KAC, ta có:
AB = AC (chứng minh trên)
chung
⇒ ΔHAB = ΔKAC (cạnh huyền – góc nhọn)
⇒ AH = AK (cặp cạnh tương ứng)
b) Xét hai tam giác vuông KAI và HAI, ta có:
AH = AK (chứng minh trên)
AI cạnh chung
⇒ ΔHAI = ΔKAI (cạnh huyền – cạnh góc vuông)
(cặp góc tương ứng)
Hay AI là tia phân giác của
Bài 66 (trang 137 – SGK Toán lớp 7 Tập 1)
Tìm các tam giác bằng nhau trên hình 148.

+ Xét hai tam giác vuông DAM và EAM có:
(giả thiết)
AM cạnh chung
⇒ ΔDAM = ΔEAM (cạnh huyền – góc nhọn)
⇒ DM = EM (cặp cạnh tương ứng)
+ Xét hai tam giác vuông DBM và ECM ta có:
MB = MC (giả thiết)
DM = EM (chứng minh trên)
⇒ ΔDBM = ΔECM (cạnh huyền – cạnh góc vuông)
+ Xét hai tam giác vuông AMB và AMC ta có:
AM cạnh chung
MB = MC (giả thiết)
AB = AD + DB = AE + EC = AC (theo các chưng minh trên)
⇒ ΔAMB = ΔAMC (cạnh – cạnh – cạnh)
Đăng bởi: THPT Nguyễn Đình Chiểu
Chuyên mục: Tài Liệu Lớp 7












