Giải Toán 7 Bài 7: Tính chất đường trung trực của một đoạn thẳng
Giải bài tập Toán 7 Bài 7: Tính chất đường trung trực của một đoạn thẳng để xem gợi ý giải các bài tập trang 76, 77 thuộc chương trình Hình học lớp 7 tập 2.
Tài liệu được biên soạn với nội dung bám sát chương trình sách giáo khoa trang 76, 77 Toán lớp 7 tập 2. Qua đó giúp học sinh lớp 7 tham khảo nắm vững hơn kiến thức trên lớp. Mời các bạn cùng theo dõi bài tại đây.
Bạn đang xem: Giải Toán 7 Bài 7: Tính chất đường trung trực của một đoạn thẳng
Lý thuyết Tính chất đường trung trực của một đoạn thẳng
A. Định lý về tính chất các điểm thuộc đường trung trực
Điểm nằm trên đường trung trực của một đoạn thẳng thì cách đều hai mút của đoạn thẳng đó.
B. Định lý đảo
 Điểm cách đều hai mút của một đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng đó.
Điểm cách đều hai mút của một đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng đó.
MA = MB ⇒ M thuộc đường trung trực của AB
Nhận xét: Từ hai định lý thuận và đảo, ta có: Tập hợp các điểm cách đều hai mút của một đoạn thẳng là đường trung trực của đoạn thẳng đó.
Giải bài tập toán 7 trang 76 tập 2
Bài 44 (trang 76 SGK Toán 7 Tập 2)
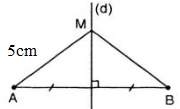
Gọi M là điểm nằm trên đường trung trực của đoạn thẳng AB, cho đoạn thẳng MA có độ dài 5cm. Hỏi độ dài MB bằng bao nhiêu?
Dựa vào định lí về tính chất của các điểm thuộc đường trung trực (định lý thuận): Điểm nằm trên đường trung trực của một đoạn thẳng thì cách đều hai mút của đoạn thẳng đó.
Điểm M thuộc đường trung trực của AB
⇒ MA = MB (định lí thuận)
Vì MA = 5cm nên MB = 5cm
Bài 45 (trang 76 SGK Toán 7 Tập 2)
Chứng minh đường thẳng PQ được vẽ như trong hình 43 đúng là đường trung trực của đoạn thẳng MN.
Gợi ý: Sử dụng định lí 2
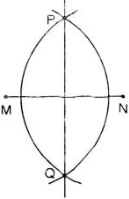
Ta có : Hai cung tròn tâm M và N có bán kính bằng nhau và cắt nhau tại P, Q.
Nên MP = NP và MQ = NQ
⇒ P; Q cách đều hai mút M, N của đoạn thẳng MN
nên theo định lí 2 : P; Q thuộc đường trung trực của MN
hay đường thẳng qua P, Q là đường trung trực của MN.
Vậy PQ là đường trung trực của MN.
Bài 46 (trang 76 SGK Toán 7 Tập 2)
Cho ba tam giác cân ABC, DBC, EBC có chung đáy BC. Chứng minh ba điểm A, D, E thẳng hàng.
Vì ΔABC cân tại A ⇒ AB = AC
⇒ A thuộc đường trung trực của BC.
Vì ΔDBC cân tại D ⇒ DB = DC
⇒ D thuộc đường trung trực của BC
Vì ΔEBC cân tại E ⇒ EB = EC
⇒ E thuộc đường trung trực của BC
Do đó A, D, E cùng thuộc đường trung trực của BC
Vậy A, D, E thẳng hàng

Giải bài tập toán 7 trang 76 tập 2: Luyện tập
Bài 47 (trang 76 SGK Toán 7 Tập 2)
Cho hai điểm M, N nằm trên đường trung trực của đoạn thẳng AB. Chứng minh ΔAMN = Δ BMN.
Vì M thuộc đường trung trực của AB
⇒ MA = MB (định lý thuận về tính chất của các điểm thuộc đường trung trực)
N thuộc đường trung trực của AB
⇒ NA = NB (định lý thuận về tính chất của các điểm thuộc đường trung trực)
Do đó ΔAMN và ΔBMN có:
AM = BM (cmt)
MN chung
AN = BN (cmt)
⇒ ΔAMN = ΔBMN (c.c.c)

Bài 48 (trang 77 SGK Toán 7 Tập 2)
Hai điểm M và N cùng nằm trên một nửa mặt phẳng bờ là đường thẳng xy. Lấy điểm L đối xứng với M qua xy. Gọi I là một điểm của xy. Hãy so sánh IM + IN với LN.
Vì L và M đối xứng qua đường thẳng xy nên xy là đường thẳng đi qua trung điểm và vuông góc với ML.
Nên đường thẳng xy là trung trực của ML.
I ∈ xy ⇒ IM = IL (theo định lý 1).
Nên IM + IN = IL + IN
– TH1: Nếu I, L, N thẳng hàng
⇒ IL + IN = LN (vì N và L nằm khác phía so với đường thẳng xy và I nằm trên xy).
⇒ IM + IN = LN
 – TH2: Nếu I không là giao điểm của LN và xy thì ba điểm I, L, N không thẳng hàng
– TH2: Nếu I không là giao điểm của LN và xy thì ba điểm I, L, N không thẳng hàng
Áp dụng bất đẳng thức tam giác vào Δ INL ta được: IL + IN > LN
mà IM = IL (cmt)
⇒ IL + IN > LN (bất đẳng thức tam giác)
⇒ IM + IN > LN

Vậy với mọi vị trí của I trên xy thì IM + IN ≥ LN
Bài 49 (trang 77 SGK Toán 7 Tập 2)
Hai nhà máy được xây dựng bên bờ một con sông tại hai địa điểm A và B (h.44). Hãy tìm trên bờ sông một địa điểm C để xây dựng một trạm bơm đưa nước về cho hai nhà máy sao cho độ dài đường ống dẫn nước là ngắn nhất?
Gọi đường thẳng xy là bờ sông cần xây trạm bơm.
⇒ Bài toán đưa về: Hai điểm A, B cố định cùng nằm trên nửa mặt phẳng bờ là đường thẳng xy. Tìm vị trí điểm C nằm trên đường xy sao cho CA + CB nhỏ nhất.

Gọi A’ là điểm đối xứng của A qua đường thẳng xy.
Theo như chứng minh ở bài 48 ta có: CA + CB = CA’ + CB ≥ A’B (A’B cố định).
⇒ CA + CB đạt ngắn nhất bằng A’B.
Dấu “=” xảy ra khi CA’+CB = A’B, tức là A’; B; C thẳng hàng hay C là giao điểm của A’B và xy.
Vậy điểm đặt trạm bơm là giao điểm của đường thẳng xy với đường thẳng A’B, trong đó A’ là điểm đối xứng với A qua xy.
Bài 50 (trang 77 SGK Toán 7 Tập 2)
Một con đường quốc lộ cách không xa hai điểm dân cư (h.45). Hãy tìm bên đường đó một địa điểm để xây dựng một trạm y tế sao cho trạm y tế này cách đều hai điểm dân cư.
Gọi A và B là hai điểm dân cư ; C là điểm đặt trạm y tế ; m là đường quốc lộ
Vì C cách đều A và B nên C thuộc đường trung trực (d) của đoạn thẳng AB
mà C ∈ m nên C là giao điểm của m và đường trung trực (d) của AB.

Gọi 2 điểm dân cư là hai điểm A, B. Để xây dựng trạm y tế ở bên đường cách đều hai điểm dân cư thì trạm y tế đó phải là giao điểm giữa con đường và đường trung trực của AB.
Bài 51 (trang 77 SGK Toán 7 Tập 2)
Cho đường thẳng d và điểm P không nằm trên d. Hình 46 minh họa cho cách dựng đường thẳng đi qua điểm P vuông góc với đường thẳng d bằng thước và compa như sau:
(1) Vẽ đường tròn tâm P với bán kính thích hợp sao cho nó có cắt d tại hai điểm A và B.
(2) Vẽ hai đường tròn với bán kính bằng nhau có tâm tại A và B sao cho chúng cắt nhau. Gọi một giao điểm của chúng là C (C ≠ P)
(3) Vẽ đường thẳng PC.
Em hãy chứng minh đường thẳng PC vuông góc với d.
Đố: Tìm thêm một cách dựng nữa (bằng thước và compa)
Vẽ hình:

a) Ta có: PA = PB (A; B nằm trên cung tròn tâm P) nên P nằm trên đường trung trực của AB.
CA = CB (C nằm trên 2 cung tròn tâm A, B bán kính bằng nhau) nên C nằm trên đường trung trực của AB.
Vậy CP là đường trung trực của AB, suy ra PC ⊥ d.
b) Một cách vẽ khác
– Lấy hai điểm A, B bất kì trên d.
– Vẽ cung tròn tâm A bán kính AP, cung tròn tâm B bán kính BP. Hai cung tròn cắt nhau tại C (C khác P).
-Vẽ đường thẳng PC. Khi đó PC là đường đi qua P và vuông góc với d.

Chứng minh :
– Theo định lí 2 :
PA = CA ( P,C cùng thuộc cung tròn tâm A bán kính PA)
⇒ A thuộc đường trung trực của PC.
PB = CB (P, C cùng thuộc cung tròn tâm B bán kính PB)
⇒ B thuộc đường trung trực của PC.
⇒ AB là đường trung trực của PC
⇒ PC ⏊ AB hay PC ⏊ d.
Đăng bởi: THPT Nguyễn Đình Chiểu
Chuyên mục: Tài Liệu Lớp 7












